Video: Kuinka ratkaiset toisen asteen yhtälöitä?
2024 Kirjoittaja: Miles Stephen | [email protected]. Viimeksi muokattu: 2023-12-15 23:35
2. asteen yhtälöiden ratkaiseminen ax2 + bx + c = 0 Neliöjuurimenetelmä Käytä neliöjuurimenetelmää, jos nox-termi on olemassa. Vastaanottaja ratkaista ax2 + bx + c = 0: 1.: Käytä neliöjuurimenetelmää, jos x-termi puuttuu. 2 : Kokeile jakaa se kahteen binomiaaliin. 3.: Käytä neliöllinen kaava (QF).
Tämän jälkeen voidaan myös kysyä, mitä ovat toisen asteen yhtälöt?
Toinen - asteyhtälöt sisältää vähintään yhden muuttujan, joka on neliöity tai korotettu potenssiin kaksi. Yksi tunnetuimmista toinen - asteyhtälöt on neliö, jossa a, b ja c ovat vakioita ja a ei ole yhtä suuri kuin 0. Toinen - asteyhtälöt on kaksi mahdollista ratkaisua: ja.
mikä on yhtälön aste? TUTKINTO AN YHTÄLÖ . The tutkinnon an yhtälö jolla ei ole enempää kuin yksi muuttuja kussakin termissä, on eksponentti suurimmasta potenssista, johon kyseinen muuttuja on korotettu yhtälö . The yhtälö . 3x - 17 = 0. on ENSIMMÄINEN- DEGREE yhtälö , koska x korotetaan vain ensimmäiseen potenssiin.
Siitä, mikä on toisen asteen polynomifunktio?
Toinen - Astepolynomifunktio . Polynomifunktio jonka yleinen muoto on f(x)=Ax2+Bx+C, missä A ≠ 0 ja A, B, C ∈ R. A toinen - astepolynomifunktio jossa kaikki termien kertoimet a:n kanssa tutkinnon alle 2 nollia kutsutaan neliöiksi toiminto.
Mikä on 2. asteen trinomi?
Toisen asteen polynomit . Toisen asteen polynomit tunnetaan myös neliöllisinä polynomit . Niiden muoto tunnetaan paraabelina. Esine, joka muodostuu, kun aparaabelia kierretään symmetria-akselinsa ympäri, tunnetaan nimellä aparaboloidi tai parabolinen heijastin. Satelliittiantenni on tyypillisesti tämän muotoinen.
Suositeltava:
Kuinka ratkaiset toisen asteen yhtälön käyttämällä nollatekijälakia?
Tästä voimme päätellä, että: Jos minkä tahansa kahden luvun tulo on nolla, niin toinen tai molemmat luvut ovat nolla. Eli jos ab = 0, niin a = 0 tai b = 0 (johon sisältyy mahdollisuus, että a = b = 0). Tätä kutsutaan nollatekijälakiksi; ja käytämme sitä usein ratkaisemaan toisen asteen yhtälöitä
Miksi 2. asteen polynomia kutsutaan toisen asteen polynomiksi?
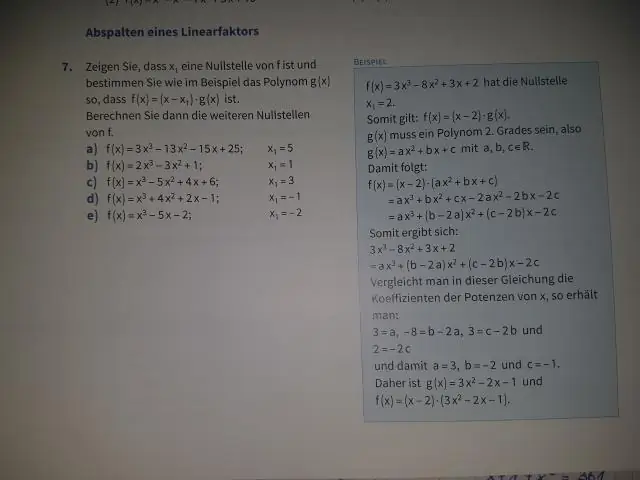
Näin on, koska quadratum on latinalainen sana neliölle, ja koska neliön, jonka sivun pituus on x, pinta-ala on x2, polynomiyhtälö, jolla on eksponentti kaksi, tunnetaan neliömäisenä yhtälönä. Laajennuksena neliöpinta on toisen asteen algebrallinen pinta
Kuinka löydät toisen asteen funktion symbolisen esityksen?
Neliöfunktiot voidaan esittää symbolisesti yhtälöllä, y(x) = ax2 + bx + c, missä a, b ja c ovat vakioita ja a ≠ 0. Tätä lomaketta kutsutaan vakiolomakkeeksi
Kuinka kirjoitat toisen asteen yhtälön C++:ssa?
Ohjelma 2: etsi a b ja c toisen asteen yhtälöstä #include #include int main(){float a,b,c; float d,juuri1,juuri2; printf('Syötä toisen asteen yhtälö muodossa ax^2+bx+c:'); scanf('%fx^2%fx%f',&a,&b,&c); d = b*b-4*a*c;
Kuinka muunnat toisen asteen yhtälön kärkimuodosta laskimeksi?
Laskin muunnokselle perusmuodosta huippumuotoon y=x2+3x+5. x2+3x+5= || +(p2)2-(p2)2=0. || a2+2ab+b2=(a+b)2. || -1⋅-1 = +1. xS = -32 = -1,5. yS=-(32)2+5=2,75