Sisällysluettelo:
Video: Kuinka muunnat toisen asteen yhtälön kärkimuodosta laskimeksi?
2024 Kirjoittaja: Miles Stephen | [email protected]. Viimeksi muokattu: 2023-12-15 23:35
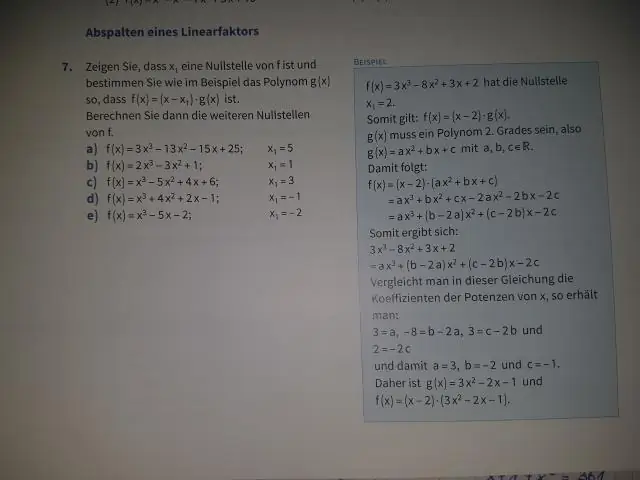
Laskin perusmuodon muuntamiseen huippumuotoon
- y=x2+3x+5.
- x2+3x+5=
- || +(p2)2-(p2)2=0.
- || a2+2ab+b2=(a+b)2.
- || -1⋅-1=+1.
- xS = -32 = -1,5.
- yS=-(32)2+5=2,75.
Kuinka sitten muunnat toisen asteen yhtälön kärkimuodoksi?
Vastaanottaja muuntaa a neliöllinen alkaen y = ax2 + bx + c muodossa to kärkimuoto , y = a(x - h)2+ k, käytät neliön viimeistelyprosessia. Katsotaanpa esimerkkiä. Muuntaa y = 2x2 - 4x + 5 sisään kärkimuoto , ja ilmoita kärkipiste . Yhtälö y = ax2 + bx + c muodossa.
Edellisen lisäksi mikä on tekijämuoto? A tekijämuotoinen muoto on suluissa oleva algebrallinen lauseke. Käytännössä a tekijämuotoinen muoto on tulojen summa … tai summien tulojen summa … Mikä tahansa logiikkafunktio voidaan esittää tekijämuotoinen muoto , ja mikä tahansa tekijämuotoinen muoto on esitys jostain logiikkafunktiosta.
Mikä on tässä suhteessa yhtälö huippupisteen löytämiseksi?
Paraabelilla on aina alin piste (tai korkein piste, jos paraabeli on ylösalaisin). Tätä pistettä, jossa paraabeli muuttaa suuntaa, kutsutaan " kärkipiste ". Jos neliö kirjoitetaan muodossa y = a(x – h)2 + k, sitten kärkipiste on piste (h, k).
Mikä on paraabelin kärki?
The Paraabelin huippupiste . The paraabelin kärki on kohta, jossa paraabeli ylittää symmetria-akselinsa. Jos x2-termin kerroin on positiivinen, kärkipiste on kaavion alin piste, U-muodon alaosassa oleva piste.
Suositeltava:
Kuinka ratkaiset toisen asteen yhtälön käyttämällä nollatekijälakia?
Tästä voimme päätellä, että: Jos minkä tahansa kahden luvun tulo on nolla, niin toinen tai molemmat luvut ovat nolla. Eli jos ab = 0, niin a = 0 tai b = 0 (johon sisältyy mahdollisuus, että a = b = 0). Tätä kutsutaan nollatekijälakiksi; ja käytämme sitä usein ratkaisemaan toisen asteen yhtälöitä
Mikä on toisen asteen yhtälön esimerkki?
Neliöyhtälö on toisen asteen yhtälö, mikä tarkoittaa, että se sisältää vähintään yhden termin, joka on neliöity. Vakiomuoto on ax² + bx + c = 0, jossa a, b ja c ovat vakioita tai numeerisia kertoimia, ja x on tuntematon muuttuja. Yksi ehdoton sääntö on, että ensimmäinen vakio 'a' ei voi olla nolla
Miksi 2. asteen polynomia kutsutaan toisen asteen polynomiksi?
Näin on, koska quadratum on latinalainen sana neliölle, ja koska neliön, jonka sivun pituus on x, pinta-ala on x2, polynomiyhtälö, jolla on eksponentti kaksi, tunnetaan neliömäisenä yhtälönä. Laajennuksena neliöpinta on toisen asteen algebrallinen pinta
Kuinka kirjoitat toisen asteen yhtälön C++:ssa?
Ohjelma 2: etsi a b ja c toisen asteen yhtälöstä #include #include int main(){float a,b,c; float d,juuri1,juuri2; printf('Syötä toisen asteen yhtälö muodossa ax^2+bx+c:'); scanf('%fx^2%fx%f',&a,&b,&c); d = b*b-4*a*c;
Kuinka muutat toisen asteen yhtälön yleisestä muodosta vakiomuotoon?
Mikä tahansa neliöfunktio voidaan kirjoittaa vakiomuodossa f(x) = a(x - h) 2 + k, jossa h ja k on annettu kertoimilla a, b ja c. Aloitetaan toisen asteen funktiosta yleisessä muodossa ja täydennetään neliö kirjoittaaksesi sen uudelleen vakiomuotoon