
- Kirjoittaja Miles Stephen stephen@answers-science.com.
- Public 2023-12-15 23:35.
- Viimeksi muokattu 2025-01-22 16:58.
From tästä voimme päätellä, että:
Jos minkä tahansa kahden luvun tulo on nolla, toinen tai molemmat luvuista on nolla. Eli jos ab = 0, niin a = 0 tai b = 0 (johon sisältyy mahdollisuus, että a = b = 0). Tätä kutsutaan Nollatekijälaki ; ja me käyttää sitä usein ratkaista toisen asteen yhtälöt.
Vastaavasti kysytään, mitkä ovat 4 tapaa ratkaista toisen asteen yhtälö?
Neljä menetelmiä toisen asteen yhtälön ratkaisemiseksi ovat factoring, käyttämällä neliöjuuria, täydentävät neliön ja neliöllinen kaava. Joten se, mistä haluan puhua nyt, on yleiskatsaus kaikista erilaisista tapoja ratkaista toisen asteen yhtälö.
Lisäksi mitä neliön täydentämisellä tarkoitetaan? Neliön viimeistely on menetelmä, jolla ratkaistaan toisen asteen yhtälö muuttamalla yhtälön muotoa niin, että vasen puoli on täydellinen neliö - kolmiosainen. Ratkaise ax2+bx+c=0 by täydentämään aukiota : 1. Muunna yhtälö siten, että vakiotermi c on yksin oikealla puolella.
Sitä paitsi, mikä on nollatekijä?
The Nollakerroin Laki Jos minkä tahansa kahden luvun tulo on nolla, toinen tai molemmat luvuista on nolla. Eli jos ab = 0, niin a = 0 tai b = 0 (johon sisältyy mahdollisuus, että a = b = 0). Tätä kutsutaan Nollakerroin Laki; ja käytämme sitä usein toisen asteen yhtälöiden ratkaisemiseen.
Mikä on toisen asteen yhtälö matematiikassa?
A toisen asteen yhtälö on yhtälö toisen asteen, mikä tarkoittaa, että se sisältää vähintään yhden termin, joka on neliöity. Vakiomuoto on ax² + bx + c = 0, jossa a, b ja c ovat vakioita tai numeerisia kertoimia, ja x on tuntematon muuttuja.
Suositeltava:
Miksi 2. asteen polynomia kutsutaan toisen asteen polynomiksi?
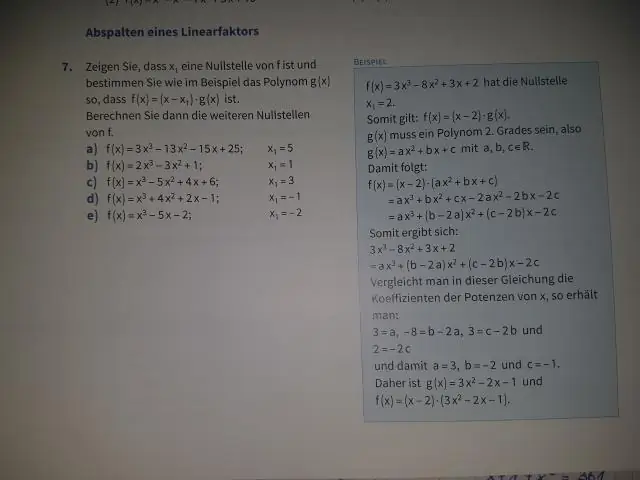
Näin on, koska quadratum on latinalainen sana neliölle, ja koska neliön, jonka sivun pituus on x, pinta-ala on x2, polynomiyhtälö, jolla on eksponentti kaksi, tunnetaan neliömäisenä yhtälönä. Laajennuksena neliöpinta on toisen asteen algebrallinen pinta
Kuinka kirjoitat toisen asteen yhtälön C++:ssa?
Ohjelma 2: etsi a b ja c toisen asteen yhtälöstä #include #include int main(){float a,b,c; float d,juuri1,juuri2; printf('Syötä toisen asteen yhtälö muodossa ax^2+bx+c:'); scanf('%fx^2%fx%f',&a,&b,&c); d = b*b-4*a*c;
Kuinka muunnat toisen asteen yhtälön kärkimuodosta laskimeksi?

Laskin muunnokselle perusmuodosta huippumuotoon y=x2+3x+5. x2+3x+5= || +(p2)2-(p2)2=0. || a2+2ab+b2=(a+b)2. || -1⋅-1 = +1. xS = -32 = -1,5. yS=-(32)2+5=2,75
Kuinka ratkaiset toisen asteen yhtälöitä?

2. asteen yhtälöiden ratkaiseminen ax2 + bx + c = 0 Neliöjuurimenetelmä Käytä neliöjuurimenetelmää, jos nox-termi on olemassa. Ratkaise ax2 + bx + c = 0: 1.: Käytä neliöjuurimenetelmää, jos x-termi puuttuu. 2.: Yritä laskea se kahteen binomiaaliin. Kolmas: Käytä toisen asteen kaavaa (QF)
Kuinka muutat toisen asteen yhtälön yleisestä muodosta vakiomuotoon?

Mikä tahansa neliöfunktio voidaan kirjoittaa vakiomuodossa f(x) = a(x - h) 2 + k, jossa h ja k on annettu kertoimilla a, b ja c. Aloitetaan toisen asteen funktiosta yleisessä muodossa ja täydennetään neliö kirjoittaaksesi sen uudelleen vakiomuotoon
