
- Kirjoittaja Miles Stephen [email protected].
- Public 2023-12-15 23:35.
- Viimeksi muokattu 2025-06-01 05:04.
Fermatin pieni lause toteaa, että jos p on alkuluku, niin mille tahansa kokonaisluvulle a luku a s - a on p:n kokonaislukukerrannainen. as ≡ a (mod p). Erikoistapaus: Jos a ei ole jaollinen p:llä, Fermatin pieni lause on sama kuin väite, että a s-1-1 on p:n kokonaislukukerrannainen.
Kuinka todistat tällä tavalla Fermatin pienen lauseen?
Olkoon p alkuluku ja mikä tahansa kokonaisluku, sitten as = a (mod p). Todiste. Tulos on trivaali (molemmat puolet ovat nollia), jos p jakaa a. Jos p ei jaa a:ta, meidän tarvitsee vain kertoa kongruenssi in Fermatin pieni lause a suorittaaksesi todistuksen loppuun.
Tiedä myös, mikä on ratkaisu Fermatin viimeiseen lauseeseen? Ratkaisu varten Fermatin viimeinen lause . Fermatin viimeinen lause (FLT), (1637), väittää, että jos n on kokonaisluku, joka on suurempi kuin 2, on mahdotonta löytää kolmea luonnollista lukua x, y ja z, joissa tällainen yhtäläisyys täyttyy, kun xn+yn on (x, y)>0 =zn.
Kun tämä otetaan huomioon, miksi Fermatin pieni lause on tärkeä?
Fermatin pieni lause on perusasia lause alkeislukuteoriassa, joka auttaa laskemaan kokonaislukujen potenssit modulo alkulukuja. Se on Eulerin erikoistapaus lause , ja on tärkeä alkeislukuteorian sovelluksissa, mukaan lukien primaalisuustestaus ja julkisen avaimen salaus.
Mitä tarkoittaa Eulerin lause?
Eulerin lause . Fermatin yleistys lause tunnetaan Eulerin lause . Yleisesti, Eulerin lause toteaa, että "jos p ja q ovat suhteellisia alkulukuja, niin ", missä φ on Eulerin totient-funktio kokonaislukuille. Toisin sanoen on ei-negatiivisten lukujen lukumäärä, jotka ovat pienempiä kuin q ja suhteellisesti alkuluku q:n suhteen.
Suositeltava:
Kuinka teet Durbin Watson -testin Minitabissa?
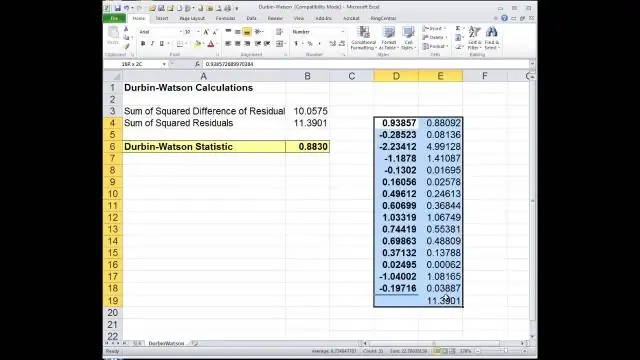
Minivälilehdellä: Napsauta Tilasto > Regressio > Regressio > Sovita regressiomalli. Napsauta "Tulokset" ja tarkista Durbin-Watson-tilasto
Kuinka teet suolalumihiutaleita kiteillä?

Ohjeet: Kiehauta vesi ja kaada se kuppiin, joka kestää kuumaa vettä. Lisää pari teelusikallista suolaa ja sekoita siveltimellä, kunnes se irtoaa. Jatka suolan lisäämistä teelusikallinen kerrallaan, kunnes se ei enää liukene ja kupin pohjassa on suolakiteitä hetken sekoittamisen jälkeenkin
Mikä aiheutti pienen jääkauden?

Pienen jääkauden vulkaaninen alkuperä. Pikku jääkausi johtui massiivisten tulivuorenpurkausten jäähdytysvaikutuksesta ja sitä ylläpitävät muutokset arktisen jääpeitteen, tutkijat päättelevät. He sanovat, että sarja purkauksia juuri ennen vuotta 1300 alensi arktisen alueen lämpötiloja tarpeeksi, jotta jäälevyt voivat laajentua
Mikä on pienen ympyrän maantiede?

Pienet ympyrät ovat ympyröitä, jotka leikkaavat maan, mutta eivät yhtä suuriksi puoliksi. Esimerkkejä pienistä ympyröistä ovat kaikki leveyspiirit paitsi päiväntasaaja, syövän trooppinen, Kauriin trooppinen alue, napapiiri ja Etelämanner ympyrä
Mikä aiheutti pienen jääkauden 400 vuotta sitten?

Pienen jääkauden vulkaaninen alkuperä. Pikku jääkausi johtui massiivisten tulivuorenpurkausten jäähdytysvaikutuksesta ja sitä ylläpitävät muutokset arktisen jääpeitteen, tutkijat päättelevät. He sanovat, että sarja purkauksia juuri ennen vuotta 1300 alensi arktisen alueen lämpötiloja tarpeeksi, jotta jäälevyt voivat laajentua
