
- Kirjoittaja Miles Stephen stephen@answers-science.com.
- Public 2023-12-15 23:36.
- Viimeksi muokattu 2025-01-22 16:58.
The toisen asteen kaavio toiminto On U- muotoinen käyrä, jota kutsutaan paraabeliksi. Se voi olla piirretty piirtämällä ratkaisuja yhtälö , etsimällä kärki ja piirtämällä valitut pisteet symmetria-akselilla tai etsimällä juuret ja kärki. Vakiomuoto a toisen asteen yhtälö on.
Miltä neliön kuvaaja näyttää tässä suhteessa?
The toisen asteen kaavio toiminto On U- muotoinen käyrä, jota kutsutaan paraabeliksi. Merkki kertoimessa a neliöllinen toiminto vaikuttaa siihen, onko kaavio avautuu ylös tai alas. X-sieppaukset ovat pisteet, joissa paraabeli leikkaa x-akselin.
Toiseksi, mikä on K vakiomuodossa? f (x) = a(x - h)2 + k , missä (h, k ) on paraabelin kärki. Tiedoksi: Eri oppikirjoissa on erilaisia tulkintoja viitteestä " vakiomuotoinen " neliöfunktiosta. (h, k ) on paraabelin kärki ja x = h on symmetria-akseli.
Mistä tiedät, onko graafi neliöllinen?
Jos ero on vakio, kaavio on lineaarinen. Jos ero ei ole vakio, mutta toinen joukko eroja on vakio, the graafi on neliöllinen . Jos erot noudattavat samanlaista mallia kuin y-arvot, the kaavio on eksponentiaalinen. Katso alla olevat esimerkit selvyyden vuoksi.
Mikä on paraabelin muoto?
Matematiikassa a paraabeli on tasokäyrä, joka on peilisymmetrinen ja suunnilleen U:n muotoinen.
Suositeltava:
Kuinka ratkaiset toisen asteen yhtälön käyttämällä nollatekijälakia?

Tästä voimme päätellä, että: Jos minkä tahansa kahden luvun tulo on nolla, niin toinen tai molemmat luvut ovat nolla. Eli jos ab = 0, niin a = 0 tai b = 0 (johon sisältyy mahdollisuus, että a = b = 0). Tätä kutsutaan nollatekijälakiksi; ja käytämme sitä usein ratkaisemaan toisen asteen yhtälöitä
Mikä on toisen asteen yhtälön esimerkki?

Neliöyhtälö on toisen asteen yhtälö, mikä tarkoittaa, että se sisältää vähintään yhden termin, joka on neliöity. Vakiomuoto on ax² + bx + c = 0, jossa a, b ja c ovat vakioita tai numeerisia kertoimia, ja x on tuntematon muuttuja. Yksi ehdoton sääntö on, että ensimmäinen vakio 'a' ei voi olla nolla
Miksi 2. asteen polynomia kutsutaan toisen asteen polynomiksi?
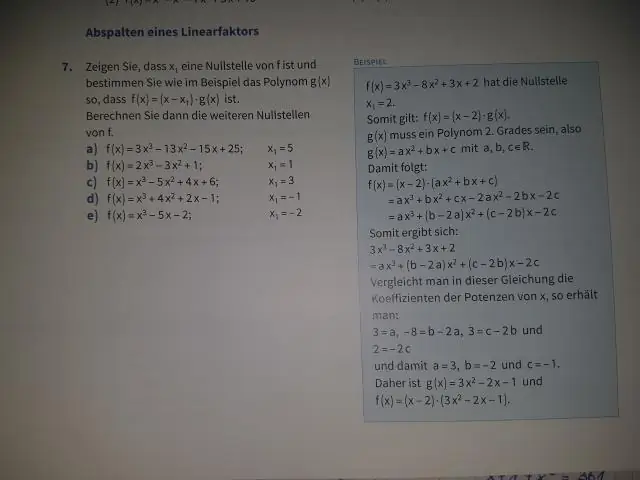
Näin on, koska quadratum on latinalainen sana neliölle, ja koska neliön, jonka sivun pituus on x, pinta-ala on x2, polynomiyhtälö, jolla on eksponentti kaksi, tunnetaan neliömäisenä yhtälönä. Laajennuksena neliöpinta on toisen asteen algebrallinen pinta
Kuinka kirjoitat toisen asteen yhtälön C++:ssa?
Ohjelma 2: etsi a b ja c toisen asteen yhtälöstä #include #include int main(){float a,b,c; float d,juuri1,juuri2; printf('Syötä toisen asteen yhtälö muodossa ax^2+bx+c:'); scanf('%fx^2%fx%f',&a,&b,&c); d = b*b-4*a*c;
Kuinka muunnat toisen asteen yhtälön kärkimuodosta laskimeksi?

Laskin muunnokselle perusmuodosta huippumuotoon y=x2+3x+5. x2+3x+5= || +(p2)2-(p2)2=0. || a2+2ab+b2=(a+b)2. || -1⋅-1 = +1. xS = -32 = -1,5. yS=-(32)2+5=2,75
