
- Kirjoittaja Miles Stephen [email protected].
- Public 2023-12-15 23:35.
- Viimeksi muokattu 2025-01-22 16:58.
The Identiteetti-ominaisuus koostuu kahdesta osasta: Lisäaine Identiteetti ja kertova Identiteetti . Lisää nolla (0) numeroon, summa on tämä luku. Kerro luku 1:llä, tuote on tämä luku. Jaa luku itsellään, osamäärä on 1.
Kysymys kuuluu myös, mikä on esimerkki identiteettiomaisuudesta?
Tietoja Transcriptistä. The identiteettiominaisuus 1 sanoo, että mikä tahansa luku kerrottuna 1:llä säilyttää sen identiteetti . Toisin sanoen mikä tahansa luku kerrottuna 1:llä pysyy samana. Syy, miksi numero pysyy samana, johtuu siitä, että kertominen 1:llä tarkoittaa, että meillä on 1 kopio numerosta. varten esimerkki , 32x1=32.
Yllä olevan lisäksi, kuinka identiteettiominaisuus vaikuttaa numeroihin? The identiteettiominaisuus lisäyksen mukaan a:n summa määrä ja nolla on määrä . Jos a on todellinen määrä , sitten a+0=a. Käänteinen omaisuutta lisäyksen mukaan minkä tahansa reaaliarvon summa määrä ja sen additiivinen käänteisarvo (vastakohta) on nolla. Jos a on todellinen määrä , niin a+(-a)=0.
Vastaavasti kysytään, mikä on identiteettiominaisuus?
Identiteettiominaisuus . The identiteettiominaisuus sillä summaus kertoo, että mihin tahansa numeroon lisätty nolla on itse numero. Nollaa kutsutaan "lisäaineeksi". identiteetti " identiteettiominaisuus kertolasku kertoo, että luku 1 kerrottuna mikä tahansa luku antaa itse luvun.
Mikä on 1:n identiteettiominaisuus?
Kertoimen mukaan identiteettiominaisuus 1 , mikä tahansa luku kerrottuna 1 , antaa saman tuloksen kuin itse numero. Sitä kutsutaan myös Identiteettiominaisuus kertolasku, koska identiteetti määrä pysyy samana. Tässä on joitain esimerkkejä identiteettiominaisuus kertomisesta.
Suositeltava:
Kuinka ratkaiset toisen asteen yhtälön käyttämällä nollatekijälakia?

Tästä voimme päätellä, että: Jos minkä tahansa kahden luvun tulo on nolla, niin toinen tai molemmat luvut ovat nolla. Eli jos ab = 0, niin a = 0 tai b = 0 (johon sisältyy mahdollisuus, että a = b = 0). Tätä kutsutaan nollatekijälakiksi; ja käytämme sitä usein ratkaisemaan toisen asteen yhtälöitä
Kuinka ratkaiset Hardy Weinbergin ongelmat?

VIDEO Tämän lisäksi, kuinka löydät P ja Q Hardy Weinbergistä? Siitä asti kun s = 1 - q ja q on tiedossa, se on mahdollista laske p yhtä hyvin. Tietäen p ja q , on helppo liittää nämä arvot Hardy - Weinberg yhtälö (p² + 2pq + q² = 1).
Kuinka ratkaiset ideaalikaasulain?

Ihanteellisen kaasulakikaava Ideaalikaasulakikaava Kysymyksiä: Vastaus: Tilavuus on V = 890,0 ml ja lämpötila on T = 21 °C ja paine on P = 750 mmHg. PV = nRT. Vastaus: Moolien lukumäärä on n = 3,00 moolia, lämpötila on T = 24°C ja paine on P = 762,4 mmHg. PV = nRT
Kuinka ratkaiset kaksivaiheiset yhtälöt esialgebrassa?

VIDEO Samoin mitkä ovat yhtälön ratkaisemisen 4 vaihetta? 4-vaiheinen opas yhtälöiden ratkaisemiseen (osa 2) Vaihe 1: Yksinkertaista yhtälön jokainen puoli. Kuten viime kerralla opimme, ensimmäinen askel yhtälön ratkaisemisessa on tehdä yhtälöstä mahdollisimman yksinkertainen.
Kuinka ratkaiset murtolukujen kertomisen ja jakamisen?
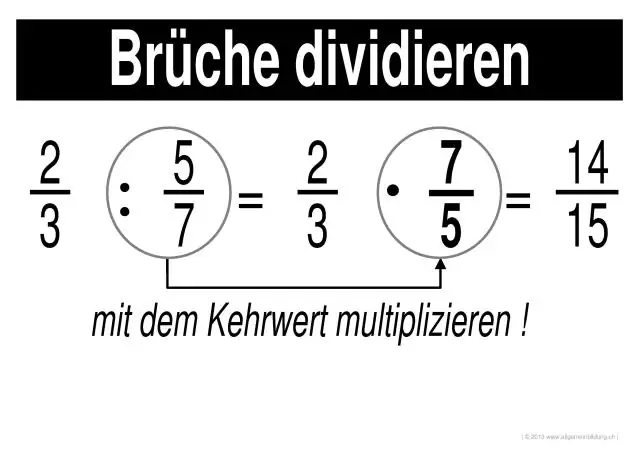
Murtolukujen kertominen ja jakaminen Vaihe 1: Kerro jokaisen murtoluvun osoittajat toisillaan (yläpuolella olevat numerot). Tulos on vastauksen osoittaja. Vaihe 2: Kerro kunkin murtoluvun nimittäjät toisilla (numerot alareunassa). Tulos on vastauksen nimittäjä. Vaihe 3: Yksinkertaista tai vähennä vastausta
