Sisällysluettelo:
Video: Kuinka ratkaiset lineaarisen yhtälön Gaussin eliminaatiolla?
2024 Kirjoittaja: Miles Stephen | [email protected]. Viimeksi muokattu: 2023-12-15 23:35
Kuinka käyttää Gaussin eliminointia yhtälöjärjestelmien ratkaisemiseen
- Voit kertoa minkä tahansa rivin kirjoittaja vakio (muu kuin nolla). moninkertaistaa rivin kolme kirjoittaja –2 antaa sinulle uuden rivin kolme.
- Voit vaihtaa mitä tahansa kahta riviä. vaihtaa riviä yksi ja kaksi.
- Voit lisätä kaksi riviä yhteen. lisää rivit yksi ja kaksi ja kirjoittaa sen sisään rivi kaksi.
Miten Gaussin eliminaatio sitten toimii?
Löyhästi sanottuna, Gaussin eliminointi toimii ylhäältä alas matriisin tuottamiseksi echelon-muodossa, kun taas Gauss -Jordania poistaminen jatkuu missä Gaussilainen keskeytetään sitten työskennellä alhaalta ylöspäin tuottaakseen matriisin supistetussa echelon-muodossa. Tekniikka havainnollistetaan seuraavassa esimerkissä.
Lisäksi, mitkä ovat Cramerin sääntömatriisit? Cramerin sääntö 2×2-järjestelmälle (kahdella muuttujalla) Cramerin sääntö on toinen menetelmä, jolla voidaan ratkaista lineaarisia yhtälöjärjestelmiä käyttämällä determinantteja. Merkintöjen suhteen a matriisi on joukko numeroita, jotka on suljettu hakasulkeilla while määräävä tekijä on joukko numeroita, joita ympäröi kaksi pystysuoraa palkkia.
Toiseksi, mikä on Gaussin eliminoinnin tarkoitus?
Gaussin eliminaatio . Wikipediasta, ilmaisesta tietosanakirjasta. Gaussin eliminaatio , joka tunnetaan myös nimellä rivivähennys, on lineaarialgebran algoritmi lineaarisen yhtälöjärjestelmän ratkaisemiseksi. Se ymmärretään yleensä toimintosarjaksi, joka suoritetaan vastaavalle kerroinmatriisille.
Mitä eroa on Gaussin ja Gauss Jordanin eliminoinnilla?
3 vastausta. Gaussin eliminaatio auttaa asettamaan matriisin rivien echelon-muotoon, while Gauss - Jordanin eliminointi asettaa matriisin supistetun rivin muotoon. Pienissä järjestelmissä (tai käsin) se on yleensä kätevämpi käyttää Gauss - Jordanin pudotus ja ratkaise erikseen jokaiselle esitetylle muuttujalle in matriisijärjestelmä.
Suositeltava:
Kuinka ratkaiset toisen asteen yhtälön käyttämällä nollatekijälakia?
Tästä voimme päätellä, että: Jos minkä tahansa kahden luvun tulo on nolla, niin toinen tai molemmat luvut ovat nolla. Eli jos ab = 0, niin a = 0 tai b = 0 (johon sisältyy mahdollisuus, että a = b = 0). Tätä kutsutaan nollatekijälakiksi; ja käytämme sitä usein ratkaisemaan toisen asteen yhtälöitä
Kuinka ratkaiset lineaarisen yhtälöjärjestelmän graafisesti?
Lineaarisen yhtälöjärjestelmän ratkaisemiseksi graafisesti piirrämme molemmat yhtälöt samassa koordinaattijärjestelmässä. Järjestelmän ratkaisu on kohdassa, jossa kaksi suoraa leikkaavat. Nämä kaksi suoraa leikkaavat (-3, -4), mikä on ratkaisu tähän yhtälöjärjestelmään
Kuinka ratkaiset lineaarisen epäyhtälön?
On kolme vaihetta: Järjestä yhtälö uudelleen siten, että "y" on vasemmalla ja kaikki muu oikealla. Piirrä viiva 'y=' (tee siitä yhtenäinen viiva y≤ tai y≥ ja katkoviiva y:lle) Varjosta viivan yläpuolelle 'suurempi kuin' (y> tai y≥) tai viivan alapuolelle 'vähemmän kuin' (y< tai y≤)
Kuinka ratkaiset lineaarisen ohjelmoinnin ongelman kulmien menetelmällä?
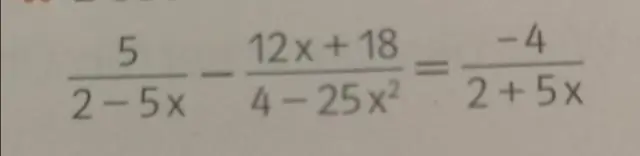
KULMAMENETELMÄ Piirrä toteutettavissa oleva joukko (alue), S. Etsi S:n kaikkien kärkien (kulmapisteiden) TARKAT koordinaatit. Arvioi tavoitefunktio P jokaisessa kärjessä Maksimi (jos se on olemassa) on pisteen suurin arvo P kärjessä. Minimi on P:n pienin arvo kärjessä
Kuinka ratkaiset lineaarisen yhtälöjärjestelmän algebrallisesti?
Käytä eliminointia ratkaistaksesi yhteisen ratkaisun kahdessa yhtälössä: x + 3y = 4 ja 2x + 5y = 5. x= –5, y= 3. Kerro jokainen ensimmäisen yhtälön termi –2:lla (saat –2x – 6y = –8) ja lisää sitten kahden yhtälön termit yhteen. Ratkaise nyt -y = -3 y:lle, ja saat y = 3