- Kirjoittaja Miles Stephen stephen@answers-science.com.
- Public 2023-12-15 23:35.
- Viimeksi muokattu 2025-01-22 16:58.
The verkkotunnus a toiminto on joukko kaikki mahdolliset syötteet toiminto . Esimerkiksi, verkkotunnus f(x)=x² on kaikki reaaliluvut, ja verkkotunnus g(x)=1/x on kaikki reaaliluvut paitsi x=0.
Kuinka löydät tästä funktion toimialueen?
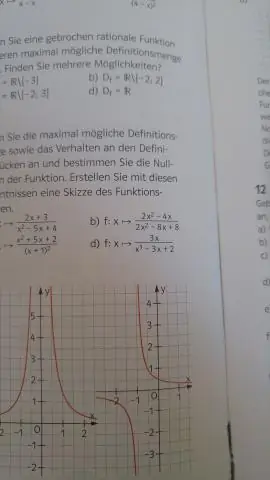
Tämän tyyppisille toiminto , verkkotunnus ovat kaikki todellisia lukuja. A toiminto murto-osalla, jonka nimittäjässä on muuttuja. Löytääksesi verkkotunnus tämän tyyppisestä toiminto , aseta pohjan arvoksi nolla ja jätä pois x-arvo, jonka löydät, kun ratkaiset yhtälön. A toiminto muuttuja radikaalin merkin sisällä.
Toiseksi, kuinka löydät funktion kaaviosta? Pystyviivatestiä voidaan käyttää määrittämään, onko a kaavio edustaa a toiminto . Pystyviiva sisältää kaikki pisteet, joilla on tietty x-arvo. Pisteen y-arvo, jossa pystysuora viiva leikkaa a kaavio edustaa lähtöä tälle tulon x arvolle.
Lisäksi, miten löydät funktion toimialueen ja alueen?
Toinen tapa tunnistaa verkkotunnus ja alue / toimintoja on käyttämällä kaavioita. Koska verkkotunnus viittaa mahdollisten syöttöarvojen joukkoon, verkkotunnus kuvaaja koostuu kaikista x-akselilla näytetyistä tuloarvoista. The alue on joukko mahdollisia lähtöarvoja, jotka näytetään y-akselilla.
Mikä on algebran toimialue?
The verkkotunnus funktio on riippumattoman muuttujan mahdollisten arvojen täydellinen joukko. Selkeässä englanniksi tämä määritelmä tarkoittaa: The verkkotunnus on joukko kaikkia mahdollisia x-arvoja, jotka saavat funktion "toimimaan" ja tulostavat todellisia y-arvoja.
Suositeltava:
Kuinka löydät trig-funktion toisen derivaatan?
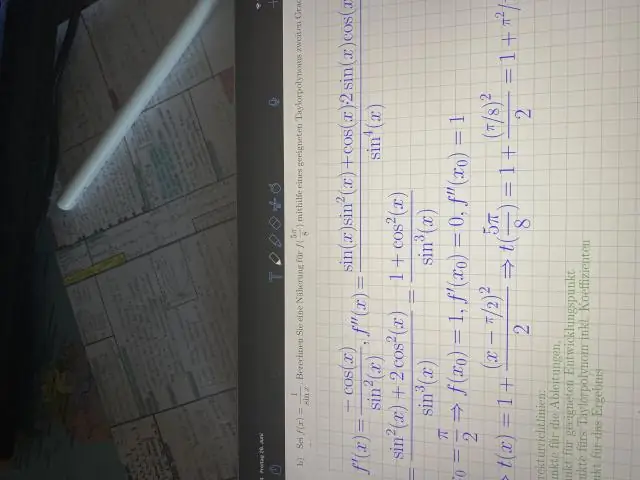
VIDEO Niin, mitkä ovat 6 trig-funktion johdannaiset? Trigonometristen funktioiden johdannaiset. Trigonometriset perusfunktiot sisältävät seuraavat 6 funktiota: sini ( synti x), kosini ( cos x), tangentti (tanx), kotangentti (cotx), sekantti (secx) ja kosekantti (cscx).
Mitkä ovat algebrallisen lausekkeen ehdot?

Muuttujia, lukuja ja operaatiosymboleja sisältävää lauseketta kutsutaan algebralliseksi lausekkeeksi. on esimerkki algebrallisesta lausekkeesta. Jokainen lauseke koostuu termeistä. Termi voi olla etumerkillinen luku, muuttuja tai vakio kerrottuna muuttujalla tai muuttujilla. Termit ovat: 5x, 3y ja 8
Kuinka löydät toisen asteen funktion symbolisen esityksen?

Neliöfunktiot voidaan esittää symbolisesti yhtälöllä, y(x) = ax2 + bx + c, missä a, b ja c ovat vakioita ja a ≠ 0. Tätä lomaketta kutsutaan vakiolomakkeeksi
Mitkä ovat rationaalisen algebrallisen lausekkeen kertomisen vaiheet?
Q ja S eivät ole 0. Vaihe 1: Kerro sekä osoittaja että nimittäjä. Vaihe 2: Kirjoita yhtenä murtolukuna. Vaihe 3: Yksinkertaista rationaalinen lauseke. Vaihe 4: Kerro loput osoittajassa ja/tai nimittäjässä olevat tekijät. Vaihe 1: Kerro sekä osoittaja että nimittäjä. Vaihe 2: Kirjoita yhtenä murtolukuna
Mitkä ovat algebrallisen lausekkeen osat?
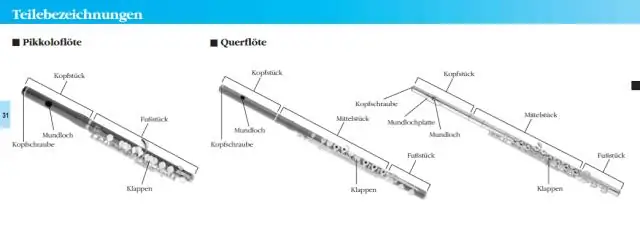
Matemaattinen lauseke on lauseke, joka sisältää lukuja, muuttujia, symboleja ja operaattoreita, jotka liittyvät yhteen-, vähennys-, kerto- ja jakolaskuihin. Jokaisella matemaattisella lausekkeella on eri osat. Kolme näistä osista ovat termejä, kertoimia ja kertoimia
