Video: Mitä eroa on parillisen t-testin ja 2-näytteen t-testin välillä?
2024 Kirjoittaja: Miles Stephen | [email protected]. Viimeksi muokattu: 2023-12-15 23:35
Kaksi- näyte t - testata käytetään, kun data on kaksi näytteet ovat tilastollisesti riippumattomia, kun taas pariksi t - testata käytetään, kun data on in sovitettujen parien muodossa. Käyttääksesi kahta näyte t - testata , meidän on oletettava, että tiedot molemmista näytteet ovat normaalijakaumia ja niillä on samat varianssit.
Ihmiset kysyvät myös, milloin pitäisi tehdä parillinen t-testi kahden näytteen t-testin sijaan?
A pariksi t - testata pitäisi olla suoritetaan kahden sijasta - näyte t - testata kun jokainen havainto yhdessä ryhmässä on kategorinen näyte ovat riippuvaisia. toisistaan riippumattomia. kunkin populaation tiedot eivät ole normaalisti jakautuneet. on riippuvainen tietystä havainnosta toisessa ryhmässä.
Lisäksi, mitä eroa on yhden näytteen testillä ja kahden näytteen testillä? yksi näyte t- testata on tilastollinen menettely, jossa halusit testata jossa väestökeskiarvosi on eri kuin vakioarvo (kiinteä luku). Kaksi näytettä t- testata on myös tilastollinen menettely, jossa olet kiinnostunut testauksessa onko nämä kaksi väestöllä on sama keskiarvo tai eri tarkoittaa.
Kysyttiin myös, mihin kahden näytteen t-testiä käytetään?
Kaksi - Näyte t - Testata . A kaksi - näyte t - testata On käytetään testaamaan ero (d0) välillä kaksi väestö tarkoittaa. Yleinen sovellus on määrittää, ovatko keinot yhtäläiset.
Pitäisikö minun käyttää parillista vai paritonta t-testiä?
A pariksi t - testata on suunniteltu vertaamaan saman ryhmän tai kohteen keskiarvoja kahdessa erillisessä skenaariossa. An pariton t - testata vertaa kahden itsenäisen tai toisiinsa liittymättömän ryhmän keskiarvoja. Vuonna an pariton t - testata , ryhmien välisen varianssin oletetaan olevan yhtä suuri. Jonkin sisällä pariksi t - testata , varianssin ei oletetaan olevan yhtä suuri.
Suositeltava:
Mitä eroa on korrelaation ja chi-neliön välillä?
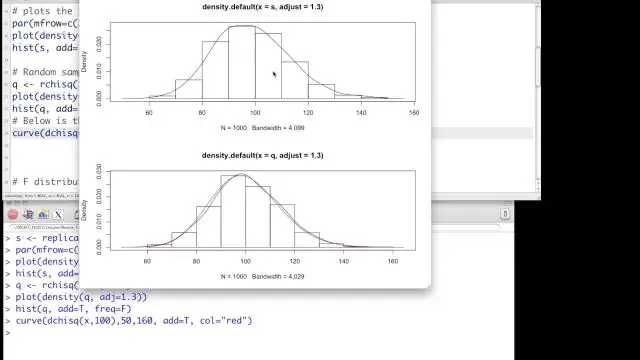
Joten korrelaatiossa on kyse kahden muuttujan välisestä lineaarisesta suhteesta. Yleensä molemmat ovat jatkuvia (tai melkein niin), mutta tapauksiin, joissa toinen on kaksijakoinen, on vaihteluita. Chi-neliö tarkoittaa yleensä kahden muuttujan riippumattomuutta. Yleensä molemmat ovat kategorisia
Mitä eroa on ilmastovyöhykkeen ja biomin välillä?
Ilmasto luokitellaan ilmakehän lämpötilan ja sateen perusteella, kun taas biomi luokitellaan ensisijaisesti yhtenäisten kasvillisuustyyppien perusteella. Ilmasto voi määrittää, mitä biomi on läsnä, mutta biomi ei yleensä hallitse tai vaikuta ilmastoon samalla tavalla
Mitä eroa on yleisen kemian ja orgaanisen kemian välillä?
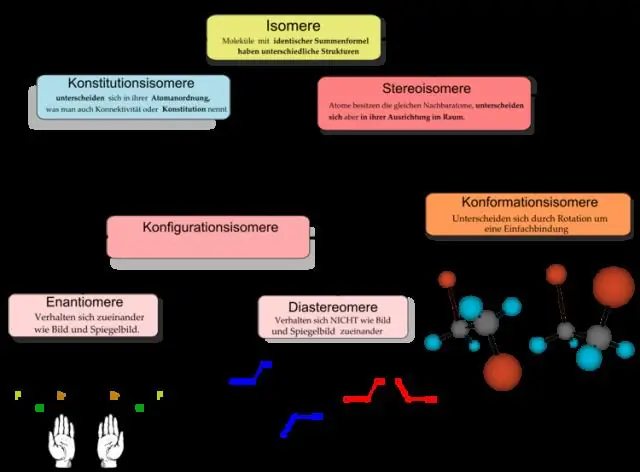
Orgaanista kemiaa pidetään kemian alatieteenä. Kun yleinen kattotermi "kemia" koskee kaiken aineen koostumusta ja muunnoksia yleensä, orgaaninen kemia rajoittuu vain orgaanisten yhdisteiden tutkimukseen
Mitä eroa on 120 ja 277 voltin välillä?
240 volttia mitataan linjasta linjaan ja 120 volttia mitataan joko linjasta nolla- tai maadoitettuun johtimeen. 480 volttia käytetään yleensä moottoreille ja joillekin laitteille, ja 277 volttia käytetään valaistukseen. Näissä järjestelmissä tarvitaan muuntaja 120 voltin pistorasian saamiseksi
Mikä on minkä tahansa kahden parillisen luvun summa?
Olkoot m ja n mitkä tahansa kaksi kokonaislukua, niin parillisen luvun määritelmän mukaan 2m ja 2n ovat molemmat parillisia lukuja, koska 2m/2 = m ja 2n/2 = n, eli kumpikin on täsmälleen jaollinen kahdella. KYLLÄ, kahden parillisen luvun summa on aina parillinen