Sisällysluettelo:
Video: Kuinka löydät sektorin kulman ympyräkaaviosta?
2024 Kirjoittaja: Miles Stephen | [email protected]. Viimeksi muokattu: 2023-12-15 23:36
1 vastaus
- Missä tahansa alalla , on otettava huomioon 3 osaa:
- Kaaren pituus on murto-osa kehästä alalla pinta-ala on murto-osa koko alueesta. The sektorikulma on murto-osa 360°:sta
- Jos alalla on 20 % ympyrädiagrammi , näiden osien vieressä on 20 % kokonaisuudesta.
- 20%×360°
- 20100×360=72°
Kuinka löydät tällä tavalla ympyrän sektorin asteen?
Selitys: Jos keskikulma on 60 astetta , jaa yhteensä 360 astetta sisällä ympyrä luvulla 60. Kerro tämä vastaavan kaaren suurella löytö koko ympärysmitta ympyrä . Käytä ympärysmittaa löytö säde, käytä sitten sädettä to löytö alue.
Tämän jälkeen kysymys kuuluu, mikä on ympyräkaavion keskikulma? Jonkin sisällä ympyrädiagrammi , eri havaintoja tai komponentteja edustavat ympyrän sektorit ja kokoympyrä edustaa kaikkien komponenttien arvojen summaa. keskikulma komponentille antaa: Keskikulma komponentille = komponentin arvoKaikkien komponenttien arvojen summa × 360°
Samoin, kuinka löydät prosenttiosuuden?
Ympyrässä on 360 astetta , joten jos haluat ilmaista kulman a prosentteina , vain jakaa kulman mittaus (in astetta ) luvulla 360 ja kerrotaan 100:lla. Käänteisesti jaa prosentteina 100:lla ja kerrotaan 360:lla.
Mikä on kaava keskikulman löytämiseksi?
Kaava S=rθ:lle Alla oleva kuva havainnollistaa säteen ja säteen välistä suhdetta keskikulma radiaaneina kaava on S=rθ, jossa s edustaa kaarenpituutta, S=rθ on keskikulma radiaaneina ja r on säteen pituus.
Suositeltava:
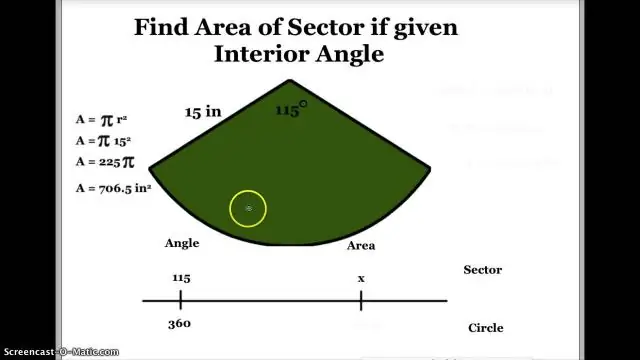
Kuinka löydät keskikulman sektorin alueen ja säteen perusteella?
Keskikulman määrittäminen sektorialueesta (πr2) × (keskikulma asteina ÷ 360 astetta) = sektorialue. Jos keskikulma mitataan radiaaneina, kaava tulee sen sijaan: sektorin pinta-ala = r2 × (keskikulma radiaaneina ÷ 2). (θ ÷ 360 astetta) × πr2. (52,3 ÷ 100π) × 360. (52,3 ÷ 314) × 360
Kuinka löydät vektorin komponenttimuodon suuruuden ja kulman perusteella?
VIDEO Kun tämä otetaan huomioon, onko 0 yksikkövektori? A yksikkövektori on vektori jonka suuruus on 1. Merkintä edustaa normia tai suuruutta vektori v. Perus yksikkövektorit olenko minä = (1, 0 ) ja j = ( 0 , 1), jotka ovat pituudeltaan 1 ja niillä on suunnat positiivista x-akselia ja y-akselia pitkin.
Kuinka löydät kaaren pituuden ja sektorin alueen?
Keskeisen kulman, jota rajoittaa suuri kaari, mitta on suurempi kuin 180°. Kaaren pituuskaavaa käytetään ympyrän kaaren pituuden määrittämiseen; l=rθ l = r θ, missä θ on radiaaneina. Sektorialue löytyy A=12θr2 A = 1 2 θ r 2, jossa θ on radiaaneina
Miten löydät kulman lisäyspostulaatin?
Kulman lisäyspostulaatin pääidea on, että jos asetat kaksi kulmaa vierekkäin, tuloksena olevan kulman mitta on yhtä suuri kuin kahden alkuperäisen kulmamitan summa. Jotta tämä postulaatti soveltuisi, myös kärjet, jotka ovat kulman kulmapisteitä, on sijoitettava yhteen
Kuinka löydät kulman tangentin yksikköympyrästä?
Yksikköympyrällä on useita eri kulmiajoista jokaisella on vastaava piste ympyrässä. Jokaisen pisteen koordinaatit antavat meille tavan löytää kunkin kulman tangentti. Kulman tangentti on yhtä suuri kuin y-koordinaatti jaettuna x-koordinaatilla