Video: Mitä eroa on lineaarisen eksponentiaalin ja neliöllisen välillä?
2024 Kirjoittaja: Miles Stephen | [email protected]. Viimeksi muokattu: 2023-12-15 23:36
Lineaarinen , eksponentiaalinen ja neliöllinen funktioita voidaan käyttää todellisen maailman ilmiöiden mallintamiseen. Algebrallisesti, lineaarinen funktiot ovat polynomifunktioita kanssa ykkösen suurin eksponentti, eksponentiaalinen funktioilla on muuttuja in eksponentti ja neliöllinen funktiot ovat polynomifunktioita kanssa kahden korkein eksponentti.
Tämän lisäksi, mikä on lineaarinen neliöllinen ja eksponentiaalinen?
Jos ensimmäinen ero on sama arvo, malli on lineaarinen . Jos toinen ero on sama arvo, malli on neliöllinen . Jos ero on otettu ennen toistuvien arvojen löytämistä yli viisi kertaa, malli voi olla eksponentiaalinen tai jokin muu erityinen yhtälö.
Toiseksi, mitä ovat lineaariset ja eksponentiaaliset funktiot? Lineaariset funktiot ovat suoria viivoja samalla eksponentiaaliset funktiot ovat kaarevia viivoja. Jos sama numero lisätään y:ään, niin toiminto on jatkuvassa muutoksessa ja on lineaarinen . Jos y-arvo kasvaa tai pienenee tietyllä prosentilla, niin toiminto On eksponentiaalinen.
On myös tiedettävä, mitä eroa on lineaarisen ja eksponentiaalisen välillä?
Lineaarinen toiminnot muuttuvat vakionopeudella yksikköväliä kohden. An eksponentiaalinen funktio muuttuu yhteisellä suhteella yhtäläisin aikavälein.
Kuinka määrität, onko funktio lineaarinen?
A lineaarinen funktio on muodossa y = mx + b tai f(x) = mx + b, missä m on kulmakerroin tai muutosnopeus ja b on y-leikkauspiste tai jossa suoran kuvaaja leikkaa y-akselin. Huomaat, että tämä toiminto on aste 1, mikä tarkoittaa, että x-muuttujan eksponentti on 1.
Suositeltava:
Mitä eroa on korrelaation ja chi-neliön välillä?
Joten korrelaatiossa on kyse kahden muuttujan välisestä lineaarisesta suhteesta. Yleensä molemmat ovat jatkuvia (tai melkein niin), mutta tapauksiin, joissa toinen on kaksijakoinen, on vaihteluita. Chi-neliö tarkoittaa yleensä kahden muuttujan riippumattomuutta. Yleensä molemmat ovat kategorisia
Mitä eroa on ilmastovyöhykkeen ja biomin välillä?
Ilmasto luokitellaan ilmakehän lämpötilan ja sateen perusteella, kun taas biomi luokitellaan ensisijaisesti yhtenäisten kasvillisuustyyppien perusteella. Ilmasto voi määrittää, mitä biomi on läsnä, mutta biomi ei yleensä hallitse tai vaikuta ilmastoon samalla tavalla
Mitä eroa on yleisen kemian ja orgaanisen kemian välillä?
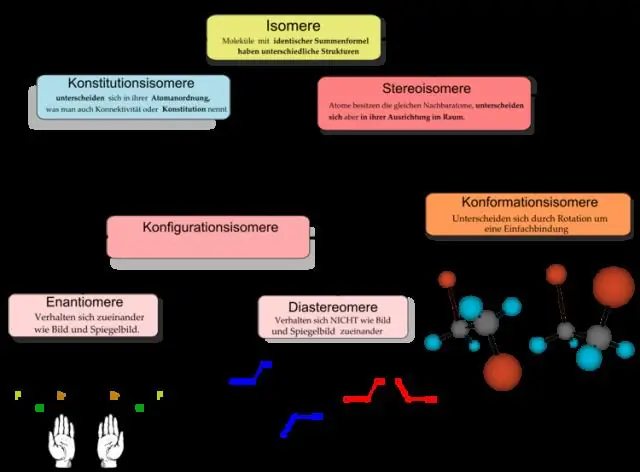
Orgaanista kemiaa pidetään kemian alatieteenä. Kun yleinen kattotermi "kemia" koskee kaiken aineen koostumusta ja muunnoksia yleensä, orgaaninen kemia rajoittuu vain orgaanisten yhdisteiden tutkimukseen
Voiko kahden lineaarisen yhtälön kuvaajien välillä olla enemmän kuin yksi leikkauspiste?
Elleivät kahden lineaarisen yhtälön kaaviot kohtaa, leikkauspisteitä voi olla vain yksi, koska kaksi suoraa voivat leikata enintään yhdessä pisteessä. Siirrä tästä pisteestä yksi yksikkö oikealle ja siirrä kaltevuuden arvoa pystysuunnassa toisen pisteen piirtämiseksi. Yhdistä sitten kaksi pistettä
Mikä tekee graafista neliöllisen?
Neliöfunktion kuvaaja on paraabeli, jonka symmetria-akseli on yhdensuuntainen y-akselin kanssa. Yhtälön y=ax2+bx+c y = a x 2 + b x + c kertoimet a,b ja c ohjaavat eri puolia siitä, miltä paraabeli näyttää piirrettynä