Video: Verrattaessa kahta populaatiota Mitä suurempi keskihajonta, sitä suurempi hajonta?
2024 Kirjoittaja: Miles Stephen | [email protected]. Viimeksi muokattu: 2023-12-15 23:36
Kun verrataan kahta populaatiota, mitä suurempi keskihajonta, sitä suurempi hajonta jakauma on edellyttäen, että kiinnostava muuttuja kuin kaksi populaatiota on sama mittasarja.
Niin, minkä kanssa standardipoikkeamaa käytetään yhdessä?
The keskihajonta On käytetään yhdessä MEAN kuvaamaan numeerisesti kellon muotoisia jakaumia. MEAN mittaa keskipisteen? jakelu, kun taas keskihajonta mittaa jakelun LEVYÄ.
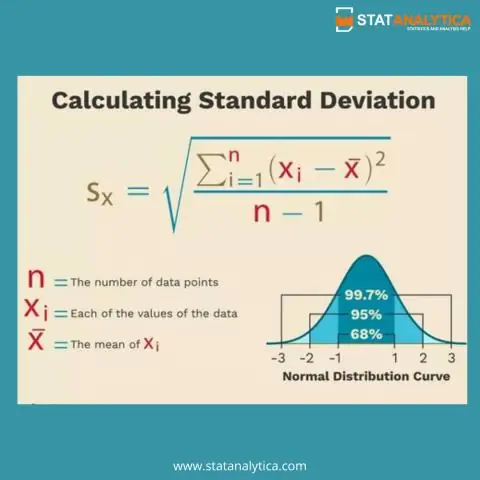
Lisäksi mikä on empiirinen sääntö tilastoissa? The empiirinen sääntö toteaa, että normaalijakaumassa lähes kaikki tiedot ovat kolmen keskihajonnan sisällä. The empiirinen sääntö voidaan jakaa kolmeen osaan: 68 % tiedoista on ensimmäisen keskipoikkeaman sisällä. 95 % on kahden standardipoikkeaman sisällä.
Mikä tässä suhteessa on vaihteluvälin rajoitus dispersion mittana?
ALUE . The alue on datan suurimman ja pienimmän havainnon välinen ero. Tämän tärkein etu dispersion mitta että se on helppo laskea. Toisaalta siinä on paljon haittoja.
Mikä edustaa havainnon keskihajonnan määrää keskiarvosta?
Z-pisteitä kutsutaan usein standardoiduksi arvoksi. Z-pisteet mittaavat keskihajonnan havaintojen määrä on ylä- tai alapuolella tarkoittaa . Esim. Z-pistemäärä 1,24 tulkitaan "tiedon arvoksi 1,24 standardipoikkeama yläpuolella tarkoittaa ."
Suositeltava:
Mitä kahta ainetta geologit käyttävät radiohiilidatauksessa?
Geologit käyttävät yleisesti radiometrisiä päivämäärämenetelmiä, jotka perustuvat tiettyjen alkuaineiden, kuten kaliumin ja hiilen, luonnolliseen radioaktiiviseen hajoamiseen luotettavina kelloina muinaisten tapahtumien päivämäärään
Onko S-neliöinen keskihajonta?
Keskihajonta (S) = varianssin neliöjuuri Keskihajonta on tilastokäytännössä yleisimmin käytetty leviämisen mitta, kun keskiarvoa käytetään laskettaessa keskiarvoa. Siten mittaukset jakautuvat keskiarvon ympärille
Mikä on taulukon keskihajonta?
Keskihajonta on yksinkertaisesti mitta siitä, kuinka hajautettu data eroaa keskiarvosta. Keskihajonnan löytäminen Tableausta edellyttää vain mittarin aggregoinnin muuttamista. Sekä perusjoukon että otoksen keskihajonnat ovat sisäänrakennettuja aggregointivaihtoehtoja
Verrattaessa näytekirjoitusta epäiltyyn asiakirjaan, asiakirjojen ikäero saa olla enintään kaksitoista kuukautta?
Kun verrataan näytekirjoitusta epäiltyyn? asiakirja, ikäero asiakirjojen välillä saa olla enintään kuudesta kahteentoista kuukautta. Riittävä määrä esimerkkejä on kriittinen vertailun tuloksen määrittämiseksi
Mikä on valon hajonta lyhyt vastaus?
Alkuperäinen vastaus: Mikä on valon hajonta? Valon hajoaminen on ilmiö, jossa valkoisen valonsäteen jakaantuminen sen seitsemään osaväriin, kun se kulkee läpinäkyvän väliaineen läpi. Sen löysi Isaac Newton vuonna 1666