
- Kirjoittaja Miles Stephen stephen@answers-science.com.
- Public 2023-12-15 23:35.
- Viimeksi muokattu 2025-01-22 16:58.
The lausunto r s on totta ehdollisen määritelmän mukaan. The lausunto s r on myös totta. Siksi lause "Kolmio on tasakylkinen silloin ja vain, jos sillä on kaksi yhtenevää (yhtä yhtäläistä) sivua" kaksiehtoinen . Yhteenveto: A kaksiehtoinen lausunto määritellään todeksi aina, kun molemmilla osilla on sama totuusarvo.
Lisäksi mikä on esimerkki kaksiehtoisesta lauseesta?
Esimerkkejä kaksiehtoisista lausunnoista The kaksiehtoisia lausuntoja nämä kaksi joukkoa olisivat: Monikulmiolla on vain neljä sivua, jos ja vain jos monikulmio on nelikulmio. Monikulmio on nelikulmio silloin ja vain, jos monikulmiolla on vain neljä sivua.
Lisäksi, mikä on kaksiehtoinen geometriassa? A kaksiehtoinen lause on yhdistelmä ehdollista lausetta ja sen käänteistä, joka on kirjoitettu jos ja vain jos -muodossa. Kaksi janaa ovat yhteneväisiä silloin ja vain, jos ne ovat yhtä pitkiä. A kaksiehtoinen on tosi, jos ja vain jos molemmat ehdolliset ovat tosia.
Milloin voit kirjoittaa kaksiehtoisen lausunnon tähän liittyen?
' Kaksiehtoiset lausunnot ovat totta lausunnot jotka yhdistävät hypoteesin ja päätelmän avainsanoihin jos ja vain jos. ' Esimerkiksi lausunto tulee ota tämä muoto: (hypoteesi) jos ja vain jos (päätelmä). Voisimme myös kirjoittaa se näin: (päätelmä) jos ja vain jos (hypoteesi).
Mitä IFF tarkoittaa Biconditional-lauseessa?
Logiikassa ja matematiikassa looginen kaksiehtoinen , joka tunnetaan joskus materiaalina kaksiehtoinen , on looginen konnektiivi, jota käytetään yhdistämään kaksi lausunnot ja muodostaa lausunto "jos ja vain jos", missä tunnetaan edeltäjänä ja sen seurauksena. Tästä käytetään usein lyhennettä " iff ".
Suositeltava:
Mikä on kaksiehtoinen lauseke logiikassa?

Kun yhdistämme kaksi ehdollista lausetta tällä tavalla, meillä on kaksiehtoinen. Määritelmä: Kaksiehtoinen väite määritellään todeksi aina, kun molemmilla osilla on sama totuusarvo. Kaksiehtoinen p q edustaa 'p jos ja vain jos q', missä p on hypoteesi ja q on johtopäätös
Mikä on lauseke, joka sisältää yhden tai useamman muuttujan?
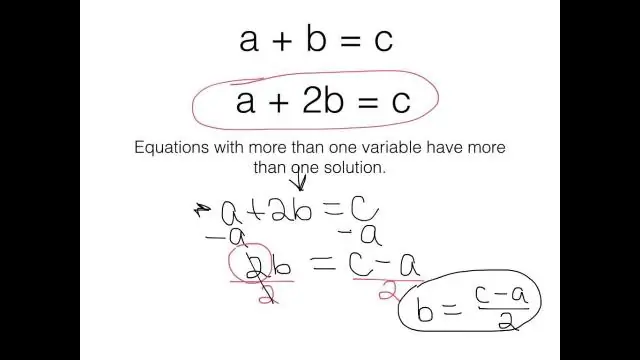
Algebrallinen lauseke on lauseke, joka sisältää yhden tai useamman muuttujan. Algebrallinen yhtälö on yhtälö, joka sisältää yhden tai useamman muuttujan
Mikä on lauseke, joka yhdistää muuttujien numerot ja vähintään yhden operaation?

Numeerinen lauseke sisältää numeroita ja operaatioita. Algebrallinen lauseke on lähes täsmälleen sama, paitsi että se sisältää myös muuttujia
Mikä on 45:n ja R:n osamäärän algebrallinen lauseke?

45:n ja r:n osamäärä on 45r. Osamäärä on jaon tulos. Esimerkiksi 84 = 2. Joten 2 on osamäärä
Mikä lauseke, joka sisältää vähintään yhden muuttujan?

Algebrallinen lauseke?: Matemaattinen lause, joka sisältää vähintään yhden muuttujan ja joskus numeroita ja operaatiosymboleja
