Sisällysluettelo:
Video: Kuinka ratkaiset Tan-identiteetit?
2024 Kirjoittaja: Miles Stephen | [email protected]. Viimeksi muokattu: 2023-12-15 23:35
Määritä tangentin eroidentiteetti käyttämällä sitä tosiasiaa, että tan(−β) = −tanβ
- Esimerkki 1: Etsi tarkka arvo rusketus 75°.
- Esimerkki 2: Varmista rusketus (180° − x) = − rusketus x.
- Esimerkki 3: Varmista rusketus (180° + x) = rusketus x.
- Esimerkki 4: Varmista rusketus (360° − x) = − rusketus x.
- Esimerkki 5: Tarkista identiteetti .
Sitä paitsi, mikä on tangentin kaava?
Missä tahansa suorakulmaisessa kolmiossa, tangentti kulma on vastakkaisen sivun pituus (O) jaettuna viereisen sivun (A) pituudella. Jonkin sisällä kaava , se on kirjoitettu yksinkertaisesti nimellä "rusketus". Usein muistetaan nimellä "SOH" - mikä tarkoittaa, että sini on vastakkainen hypotenuusaan nähden.
Lisäksi, kuinka kirjoitat tangentin uudelleen? Voit kirjoittaa sinifunktion uudelleen tangentin suhteen seuraavasti:
- Aloita suhdeidentiteetillä, joka sisältää sinin, kosinin ja tangentin, ja kerro kumpikin puoli kosinilla saadaksesi sini yksin vasemmalla.
- Korvaa kosini sen käänteisfunktiolla.
- Ratkaise Pythagoraan identiteettirusketus2θ + 1 = sek2θ sekantille.
Mikä on kaksoiskulmakaava tässä suhteessa?
Tietoja Transcriptistä. Kosini kaksoiskulmakaava kertoo meille, että cos(2θ) on aina yhtä suuri kuin cos²θ-sin²θ. Esimerkiksi cos(60) on yhtä suuri kuin cos²(30)-sin²(30). Voimme käyttää tätä identiteettiä lausekkeiden uudelleenkirjoittamiseen tai ongelmien ratkaisemiseen.
Mikä on tangentin identiteetti?
Summa identiteetti varten tangentti johdetaan seuraavasti: Eron määrittämiseksi identiteetti varten tangentti , käytä sitä tosiasiaa rusketus (−β) = −tanβ. Kaksoiskulma identiteetti varten tangentti saadaan käyttämällä summaa identiteetti varten tangentti . Puolikulma identiteetti varten tangentti voidaan kirjoittaa kolmessa eri muodossa.
Suositeltava:
Kuinka ratkaiset toisen asteen yhtälön käyttämällä nollatekijälakia?
Tästä voimme päätellä, että: Jos minkä tahansa kahden luvun tulo on nolla, niin toinen tai molemmat luvut ovat nolla. Eli jos ab = 0, niin a = 0 tai b = 0 (johon sisältyy mahdollisuus, että a = b = 0). Tätä kutsutaan nollatekijälakiksi; ja käytämme sitä usein ratkaisemaan toisen asteen yhtälöitä
Kuinka ratkaiset Hardy Weinbergin ongelmat?
VIDEO Tämän lisäksi, kuinka löydät P ja Q Hardy Weinbergistä? Siitä asti kun s = 1 - q ja q on tiedossa, se on mahdollista laske p yhtä hyvin. Tietäen p ja q , on helppo liittää nämä arvot Hardy - Weinberg yhtälö (p² + 2pq + q² = 1).
Kuinka ratkaiset ideaalikaasulain?
Ihanteellisen kaasulakikaava Ideaalikaasulakikaava Kysymyksiä: Vastaus: Tilavuus on V = 890,0 ml ja lämpötila on T = 21 °C ja paine on P = 750 mmHg. PV = nRT. Vastaus: Moolien lukumäärä on n = 3,00 moolia, lämpötila on T = 24°C ja paine on P = 762,4 mmHg. PV = nRT
Kuinka ratkaiset kaksivaiheiset yhtälöt esialgebrassa?
VIDEO Samoin mitkä ovat yhtälön ratkaisemisen 4 vaihetta? 4-vaiheinen opas yhtälöiden ratkaisemiseen (osa 2) Vaihe 1: Yksinkertaista yhtälön jokainen puoli. Kuten viime kerralla opimme, ensimmäinen askel yhtälön ratkaisemisessa on tehdä yhtälöstä mahdollisimman yksinkertainen.
Kuinka ratkaiset murtolukujen kertomisen ja jakamisen?
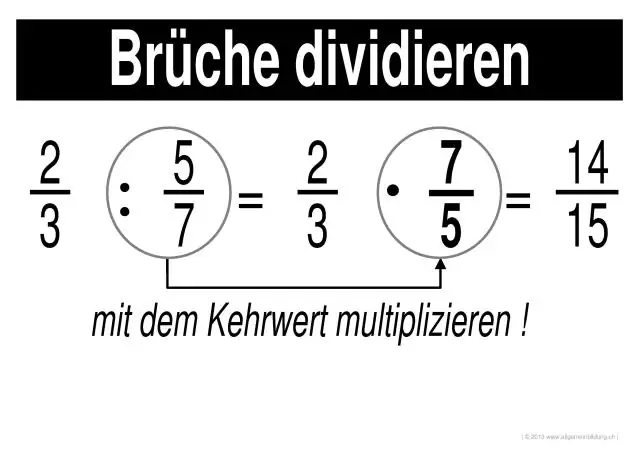
Murtolukujen kertominen ja jakaminen Vaihe 1: Kerro jokaisen murtoluvun osoittajat toisillaan (yläpuolella olevat numerot). Tulos on vastauksen osoittaja. Vaihe 2: Kerro kunkin murtoluvun nimittäjät toisilla (numerot alareunassa). Tulos on vastauksen nimittäjä. Vaihe 3: Yksinkertaista tai vähennä vastausta